Facebook Twitter Google Plus Linkedin Instagram YouTube Pinterest Tumblr VK RSS

Month: July 2019

Bayes’ Theorem in three pictures

sunnyLeave a comment

Note: This post was back-ported from LessWrong. You can find the original here.

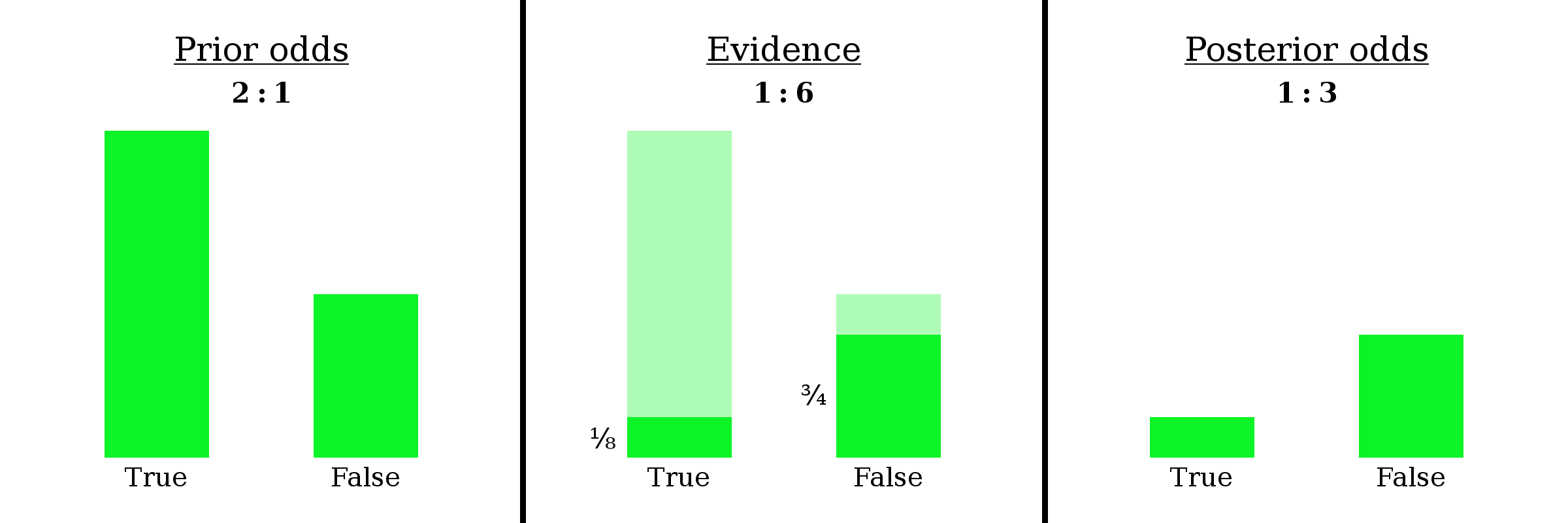
Let’s say you have a belief — I’ll call it “B” for “belief” — that you would assign 2:1 odds to. In other words, you consider it twice as likely that B is true than that B is false. If you were to sort all possible worlds into piles based on whether B is true, there would be twice as many where it’s true than not.

Then you make an observation O, which you estimate to have had different probabilities depending on whether B is true. In fact:

  • If B is true, then O had a 1/8 chance of occurring.
  • If B is false, then O had a 3/4 chance of occurring.

In other words:

  • O occurs in 1/8 of the worlds where B is true.
  • O occurs in 3/4 of the worlds where B is false.

We know you’re in a world where O occurred — you just saw it happen! So let’s go ahead and fade out all the worlds where O didn’t occur, since we know you’re not in one of them. This will slash the “B is true” pile of worlds down to 1/8 of its original size and the “B is false” pile of worlds down to 3/4 of its original size.

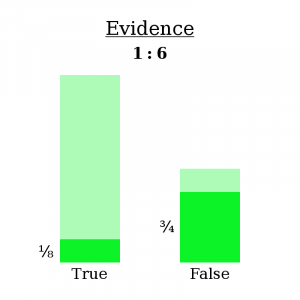
Why did I write Evidence: 1:6 at the top? Let’s ignore that for a second. For now, it’s safe to throw away the faded-out worlds, because, again, we now know they aren’t true.

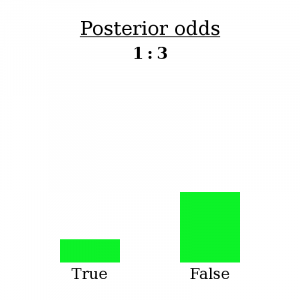
I’m going to make a bold claim: having made observation O, you have no choice but to re-asses your belief B as having 1:3 odds (three times as likely to be false than true).

How can I say such a thing? Well, initially you assigned it 2:1 odds, meaning that you thought there were twice as many possible worlds where it was true than where it was false. Having made observation O, you must eliminate all the worlds where O doesn’t happen. As for the other worlds, if you considered them possible before, and O doesn’t contradict them, then you should still consider them possible now. So there is no wiggle room: an observation tells you exactly which worlds to keep and which to throw away, and therefore determines how the ratio of worlds changes — or, how the odds change.

What about “Evidence: 1:6”?

Well, first notice that it doesn’t really matter how many worlds you’re considering total — what matters is the ratio of worlds in one pile to the other. We can write 2:1 odds as the fraction 2/1. The numerator represents the “B is true” worlds and the denominator represents the “B is false” worlds. Then, when you see the evidence, the numerator gets cut down to 1/8 of its initial size, and the denominator gets cut down to 3/4 of its initial size.

We can write this as an equation:

(2 ∗ 1/8) / (1 * 3/4) = 1/3

Now notice something else: it also doesn’t matter what the actual likelihood of observation O is in each type of world. All that matters is the ratio of likelihoods of O between one type of world and the other. O could just as well have been exactly 10 times less likely in both scenarios…

(2 ∗ 1/80) / (1 * 3/40) = 1/3

…and our final odds come out the same.

That’s why we write the evidence as 1:6 — because only the ratio matters.

This — the fact that each new observation uniquely determines how your beliefs should change, and the fact that this unique change is to multiply by the ratio of likelihoods of the observation — is Bayes’ Theorem. If it all seems obvious, good: clear thinking renders important theorems obvious.

For your viewing pleasure, here’s a combined picture of the three important diagrams.

And here’s a version without the numbers and here’s a version where the bars aren’t even labeled.

An example

On the LessWrong version of this post, user adamzerner suggested I add a concrete example. I’m happy to oblige!

Example: Mahendra has been found dead in his home, killed by a gunshot wound. Police want to know: was this a suicide or a homicide?

The first step is to establish your prior; in other words, what odds [homicide : suicide] do you assign this case right off the bat?

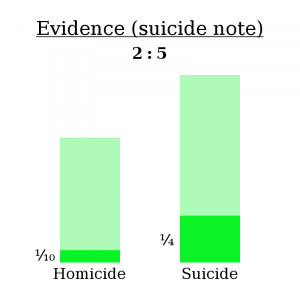
Well, according to Vox, about 40% of gun-related deaths are homicides and 60% are suicides. The number has varied a bit throughout the years, but let’s go ahead and use this figure. A 40%/60% chance equates to 2:3 odds — for every two homicides by gun, there are three suicides by gun. This is called the base rate, and it will serve as our prior odds.

It’s worth repeating that what you see above represents the fact that, if you sorted all possible worlds into piles based on Mahendra’s cause of death, you would see three in the “suicide” pile for every two in the “homicide” pile. (It’s okay if there are other modes of death under consideration too, such as “accident” — the same logic would still apply! For simplicity, I’ll just use these two.)

After a bit of investigation, a some evidence has turned up — a suicide note! Open and shut case, right?

Think again. Some murderers are smart — they’ll plant a fake suicide node at the scene of the crime to cover their tracks. I couldn’t find an exact statistic, but let’s say about 1/10 murderers think to do this.

Also, not every suicide has a note. In fact, Wikipedia reports that only about 1/4 of suicides include a note.

In other words:

  • If Mahendra’s death was a homicide, there was a 1/10 chance of finding a note.
  • If Mahendra’s death was a suicide, there was a 1/4 chance of finding a note.

So now, let’s follow the same process as before.


Here’s the math bit:

(2 ∗ 1/10) / (3 * 1/4) = 4/15

So, as expected, finding a suicide note makes the “homicide” explanation less likely — 4:15 odds compared to 2:3 odds, or about a 79% chance of suicide compared to a 60% chance initially.

However, be aware that this isn’t because most suicides include a note. In fact, most suicides don’t include a note. The reason it makes suicide more likely is that even fewer homicides include a note. It’s not true that “most suicides have a note”, but it is true that “suicides are more likely to produce a note than homicides are”. That’s what makes for proper bayesian evidence.

Why it feels like everything is a trade-off

sunnyLeave a comment
Note: This post was back-ported from LessWrong. You can find the original here.

Example of a trade-off

I’m a programmer. I’m also a design prude. I’m also lazy. This all means that I spend a lot of my time chasing some different metrics in my code:

  1. How easy it is to read.
  2. How long it takes to run.
  3. How long it takes to write.
  4. …

These metrics are often at odds with one another. Just the other day I had to make a trade-off involving a function I’d written to evaluate a polynomial at a given point. Originally, it was written in a way that I felt was self-explanatory: it looped over the derivatives-at-zero of the polynomial, which were passed in as a list, and summed up the appropriate multiples of powers of x — a Taylor sum. Pseudo-code:

def apply_polynomial( deriv, x ):
    sum = 0
    for i from 0 to length( deriv ):
        sum += deriv[i] * pow(x, i) / factorial(i)
    return sum

It turned out that this function was a significant bottleneck in the execution time of my program: about 20% of it was spent inside this function. I was reasonably sure that the pow and factorial functions were the issue. I also knew that this function would only ever be called with cubics and lower-degree polynomials. So I re-wrote the code as follows:

def apply_cubic( deriv, x ):
    sum = 0
    len = length( deriv )

    if len > 0:
        sum += deriv[0]
        if len > 1:
            sum += deriv[1] * x
            if len > 2:
                square = x * x
                sum += deriv[2] * square / 2
                if len > 3:
                    cube = square * x
                    sum += deriv[3] * cube / 6

    return sum

Sure enough, this improved the runtime significantly — by nearly the whole 20% that had been being spent inside this function. But notice that the code no longer contains the elements that define a Taylor sum: the loop is gone, and the factorials (0!, 1!, 2!, 3!) have been replaced with their values (1, 1, 2, 6). It also isn’t obvious why the length comparisons stop at 3. The code no longer explains itself, and must be commented to be understood. Readability has been sacrificed on the altar of efficiency.

Question

Why am I cursed so? Why can’t these metrics go hand-in-hand? And in general, why am I always doing this sort of thing? Sacrificing flavor for nutrition in the cafeteria, sacrificing walking-speed for politeness on a crowded sidewalk? Why are my goals so often set against one another?

Answer

Let’s take a second to think about what a trade-off is.

Suppose you’re faced with a problem to solve. You have two solutions in mind (Solution A & Solution B), and you have two metrics (Metric 1 & Metric 2) by which to judge a solution. A trade-off occurs when the solution that scores better along Metric 1 scores worse along Metric 2:

For example:

Of course, there need not be only two possible solutions. Maybe I’m willing to spend two hours working on improving this function, and depending on what I focus on, I could achieve any of the following balances:

And — argh! The correlation is negative! Why!

Well, there’s a reason, and the reason is that this isn’t the full picture. This is:

See, there are a whole bunch of ways to write the code that are neither as efficient nor as readable as one of the filled-in circles on the perimeter. But I would never choose any of those ways, for obvious reasons. And if a new solution occurs to me that beats out some of my old solutions along both metrics…

…then this new solution would replace all the solutions strictly worse than it, which in turn would become part of the mass that resides below the curve:

No matter how many new solutions are introduced into the mix, and no matter by how far they out-perform the old solutions, the outer frontier of non-dominated solutions must have negative slope everywhere. A step to the right along this line must be accompanied by a step downward, because if it isn’t, then the solution you just stepped off of is dominated by the one you just stepped onto, so the former wasn’t on the line.

It doesn’t take any math to generalize this result to situations where you have more than two metrics. Any solution that is dominated by another solution will be thrown out, so the options you end up considering form a set where no element dominates another, a.k.a. one where a gain along one metric entails a loss along at least one other, a.k.a. a trade-off. Throwing out obviously-poor solutions is easy (and is sometimes done subconsciously when you’re working in your domain of expertise, or done by other people before a decision gets to you), but weighing the remaining options usually takes some consideration. So, our subjective experience is that we spend most of our time and energy thinking about trade-offs. Q.E.D.

Note: On the LessWrong post, the user Dagon has written a comment explaining something that I meant to make more explicit in this post. Since they’ve expressed it better than I can, I’m just going to copy-paste their comment here:

One reason that most of your actual decisions involve tradeoffs is that easy no-tradeoff decisions get made quickly and don’t take up much of your time, so you don’t notice them. Many of the clear wins with no real downside are already baked into the context of the choices you’re making. For the vast majority of topics you’ll face, you’re late in the idea-evolution process, and the trivial wins are already in there.